An Optimal Control Problem

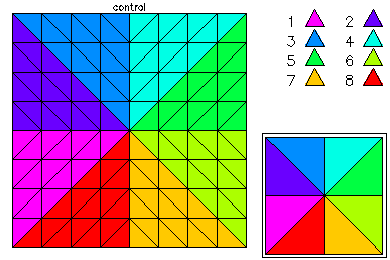
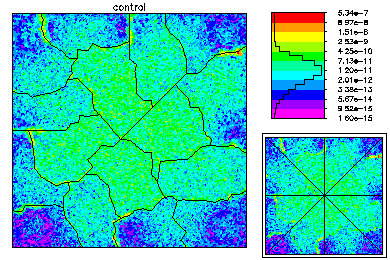
In this example, we solved an optimal control problem on the unit square. The PDE constraint was a Poisson equation, and the state variable satisfied homogeneous Dirichlet boundary conditions. The control was subject to box inequality constraints, which were handled via an interior point method.

This problem was solved using cubic finite elements. Parallel adaptive meshing using 16 processors was used to create a final global mesh with approximately 42K vertices and 370K degrees of freedom in each variables, or a total of about 1.1 million unknowns. Above is the initial coarse 9 x 9 mesh.

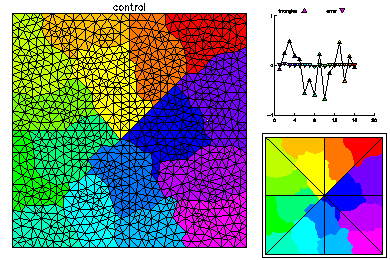
The initial mesh was adaptively refined on one processor to 1000 vertices. This mesh was partitioned for 16 processors according to equal error, where the error is estimated via an a posterior error estimator. On the right the load balance is shown without element edges lined with black, and elements are colored according to size.

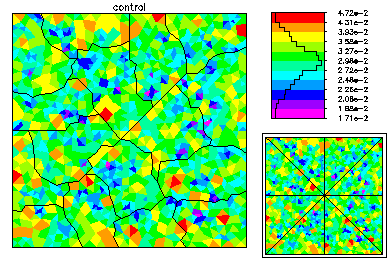
The global mesh has about 42K vertices. On the left is the global mesh colored by size. On the right is the global mesh colored by element error.

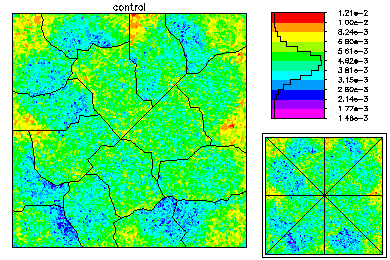
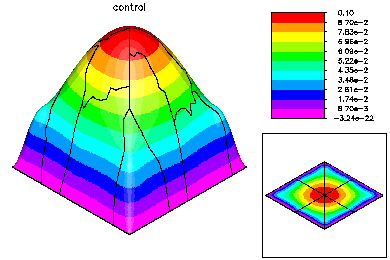
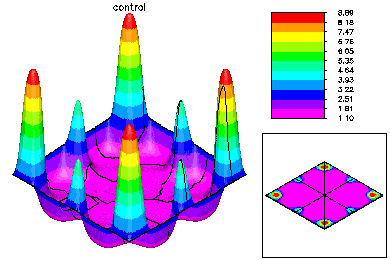
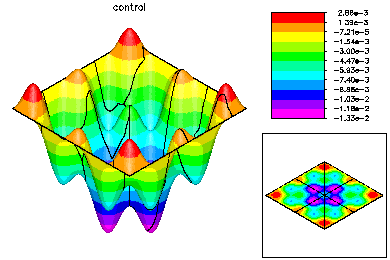
The global mesh has about 370K degrees of freedom in each of three unknown functions. On the top left is the state variable on the global fine mesh. On the top right is the optimal control. Below is the Lagrange multiplier.