SOFTWARE
PLTMG 13.0 is a package for solving elliptic partial differential equations in general regions of the plane. It is based on a family of continuous Lagrange triangular finite elements. PLTMG features options for adaptive h, p, and hp refinement, coarsening, and mesh moving. PLTMG employes several algebraic multilevel solvers for the resulting systems of linear equations. PLTMG provides a suite of continuation options to handle PDEs with parameter dependencies. It also provides options for solving several classes of optimal control and obstacle problems. The package includes an initial mesh generator and several graphics packages. Support for the Bank-Holst parallel adaptive meshing paradigm and corresponding domain decomposition solver are also provided. PLTMG is provided as Fortran90 (and a little C) source code. The code has an interface to MPI. The MPI interface requires libraries that are NOT provided as part of the PLTMG package. PLTMG 13.0 uses Chris Deotte's package WEBGUI 1.0 as its graphical user interface. WEBGUI 1.0 is included as part of the PLTMG source code, but is also available independently. PLTMG is also available from Netlib. MPICH is available from the MPICH homepage.
Multigraph 2.1 is an algebraic multilevel solver for large sparse systems of linear equations. The package takes as input just the system matrix in a sparse matrix format and constructs a hierarchy of coarse matrices based on the sparse matrix graph. The multigraph solver is written in Fortran90 and is based on the Fortran77 solver included in the PLTMG 9.0 package. The Multigraph 2.1 distribution contains the basic solver routines that can be incorporated into user applications, and a driver program with a web browser interface (WEBGUI 1.0) and graphics package that can be used independently to demonstrate and test the solver. The directory Matrix 1 contains 18 sparse linear system files corresponding to 6 elliptic PDEs on irregular regions with nonuniform adaptive meshes. The directory Matrix 3 contains 21 sparse linear system files corresponding to 7 constant coefficient PDEs on uniform square meshes. In both directories, each PDE appears for 3 different values of N.
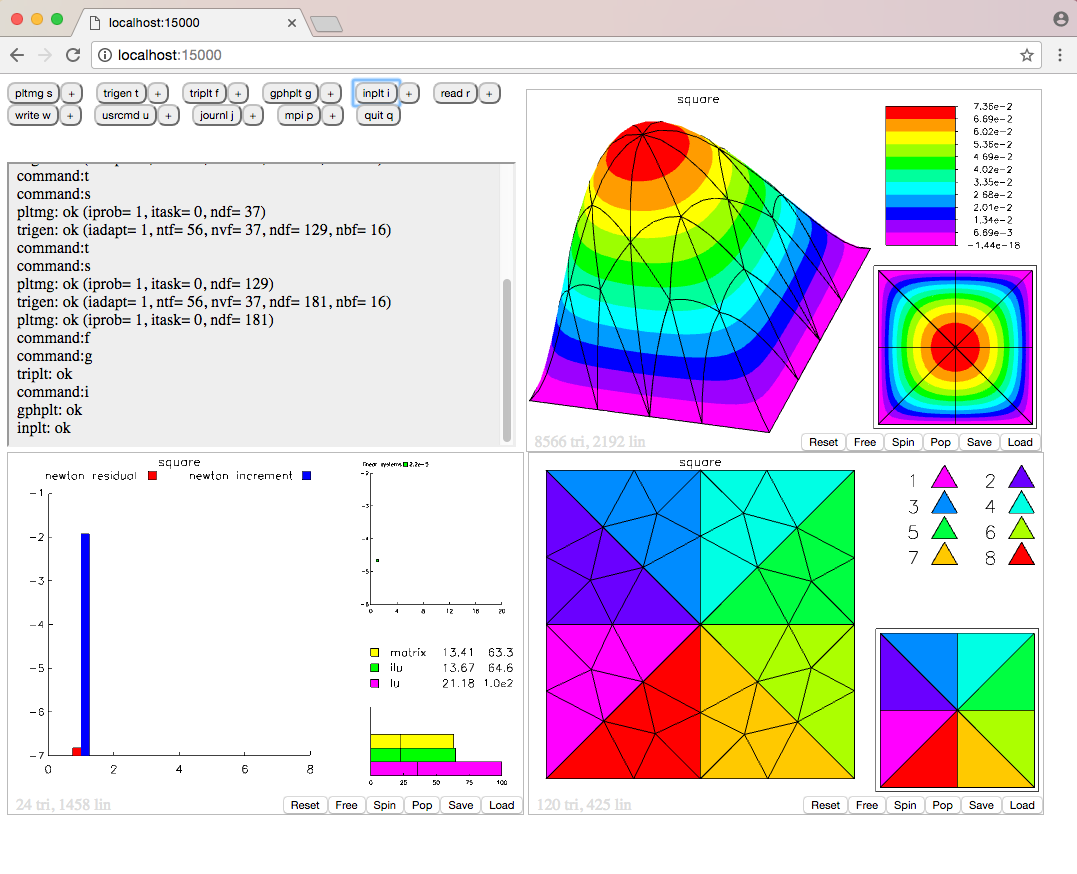
WEBGUI is a C language library that creates for your software a graphical user interface (GUI) after only a few library function calls. WEBGUI is platform independent because it displays everything in any standard web browser. And WEBGUI allows the interface to reside on either the local machine or a remote machine. WEBGUI works by enabling your program to mimic a web server. When your program calls the library routine "webstart(int x)", a new thread is created which sets up a web server and begins listening on port x. Both your program and the web server run on the same host machine. Using any standard web browser either locally or remotely, enter the URL of the host machine. Then, the web browser will display a set of controls. The web browser is in constant communication with your software running on the host machine. All of your software's output will be displayed in the web browser and all input you provide in the web browser will be sent to your software. Read the manual WEBGUI.pdf for more information. Click the image above for an example. |